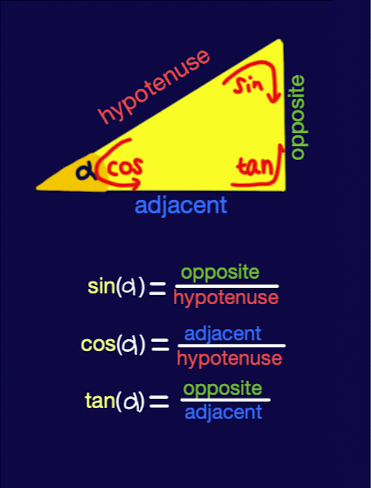
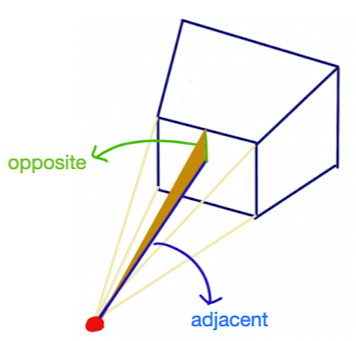
---

1️⃣ 삼각함수(trigonometric function)

---

2️⃣ 피타고라스의 법칙

• 피타고라스의 법칙은 직각삼각형의 빗변을 구하는 대중적인 수학공식 입니다.

• 우리는 이 공식을 물체(기둥)와의 거리(adjacent)를 구하는데 이용할 계획입니다.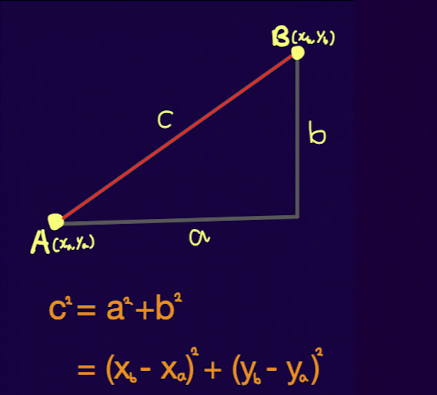

• 위의 그림처럼 두점의 좌표를 알고 있으면 쉽게 피타고라스의 법칙을 이용하여 거리를 구할 수 있습니다.

< 임시로 구현한 피타고라스식 >

distanceAB = sqrt((B_x - A_x) * (B_x - A_x) + (B_y - A_y) * (B_y - A_y));

---

3️⃣ 각도의 다양한 표현방법

• 1라디안(radians)은 원의 반지름과 호의 길이를 같게 했을 때의 각도를 말합니다.

• 180º는 약 3.14radian이며 兀라고 합니다.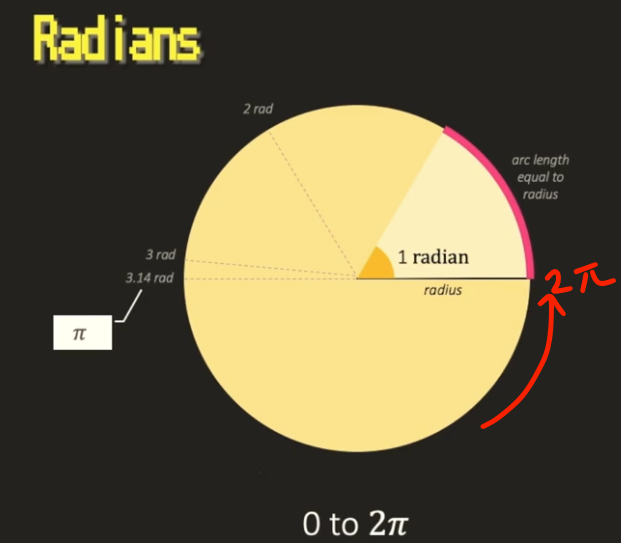

• 라디안값 혹은 각도를 구하는 함수를 다음과 같이 간단하게 구현할 수 있습니다.

• 이러한 각도계산법을 이용하여 각 광선(ray)의 각도를 구할 수 있습니다.
  (가독성을 위해 javascript문법을 이용 추후의 함수들도 먼저 javasciprt로 구현한 뒤 최종적으로 C언어로 구현할 예정입니다.)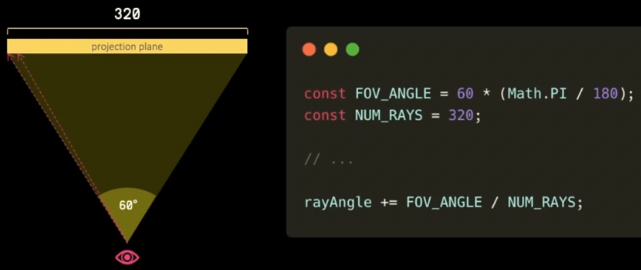

• 우리가 구현할 cub3d의 해상도가 320 x 200이라고 한다면 위와 같이 60도를 320등분한식(라디안변환)을 만들 수 있습니다.
• 그리고 'rayAngle'라는 변수를 두어 각광선의 각도만큼 순차적으로 늘려가면서 계산을 할 수 있게 됩니다.
• 320 x 200해상도에서 각광선 사이의 각도는 60º / 320이 될 것입니다.