[ft_printf](9)부동소수점(IEEE표준 표현 방식)
이번 포스트는 (ft_print)부동소수점(IEEE표준 표현 방식)에 관한 내용입니다.
1️⃣ 부동소수점(IEEE 754표준)
(1) 부동소수점 오차
C언어에서의 부동소수점표현 방식은 IEEE 754표준방식을 따르고 있습니다.
( IEEE에 대한 자세한 내용 🖝🖝 IEEE - 나무위키 )다음 예시에서 볼 수 있듯이 0.01을 100번 더했지만 1로 딱 떨어지지않고 오차가 발생했습니다.
< 부동소수점 오차 예시>
int main(void)
{
double num = 0.01;
double result;
for (int i = 0; i < 100; i++)
{
result += num;
}
printf("%.20f\n", result); // 소수점 20번째까지 출력
}
1.00000000000000066613
(2) 실수를 컴퓨터로 입력하는 방식(IEEE)
- IEEE 754표준은 32, 64, 43, 79비트에서 실수형표현 형식에 대해 정의하고 있습니다. 그중에서 32, 64비트에 대해서 알아보겠습니다.
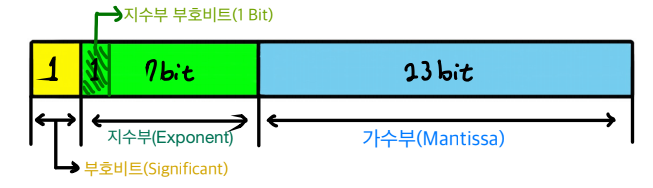
< 32비트 부동소수점 표현 >
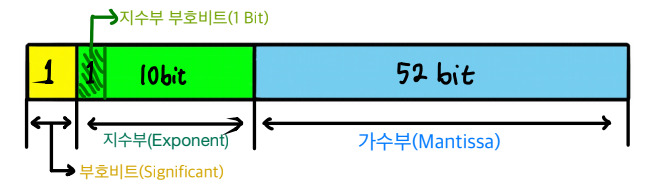
< 64비트 부동소수점 표현 >
[ 부호비트(Significant) ]
- 양수면 0, 음수면 1이 됩니다.
[ 지수부(Exponent) ]
- 32비트의 경우 8비트, 64비트의 경우 11비트를 지수부에 사용합니다.
- 입력받은 값을 2진법으로 표현한 뒤
1.xxx...의 형태가 될때까지 2를 곱하거나 나누고 2의 거듭제곱을 곱하는 형태로 따로 분리 해줍니다.
(만약 1011.111(2)이라면 1.011111 x 2^3) 2^3에서 2의 승수인 3을 지수부에 입력해줍니다. 지수부에도 부호비트로 1비트를 사용한다고 위의 그래프에 표현했지만 실질적으로는 127(127 = 2^0)을 기준으로 음수와 양수로 나눠지게 됩니다.2^3의 경우 +3승이므로 130 (127 + 3)이며 지수부(32비트기준)에10000010로 적히게 됩니다.
[ 가수부(Mantissa) ]
- 32비트의 경우 23비트, 64비트의 경우 52비트를 가수부에 사용합니다.
- 지수부에 2의 승수를 입력하고 남은
1.xxxxxx...부분을 가수부에 입력하게 됩니다. 여기서1.부분은 공통된 부분이기 때문에 최종적으로xxxxx...부분을 가수부에 입력하게 됩니다.
< 부동소수점 IEEE표준으로 만드는 과정 예시(32비트) >
100011.01(2)
1.0001101(2) x 2^5
1(부호) + 10000101(지수부) + 0001101(가수부)
/*-------최종 부동소수점 입력형태-------*/
110000101000110100000...
2️⃣ 부동소수점(부호비트, 지수부, 가수부)출력
- 부동소수점출력하기 위해서는 double형의 변수를 문자형으로 변환하는 과정이 필요합니다.
- 하지만 위에서 봤듯이 부호비트, 지수부, 가수부 부분별로 일정의 규칙을가지고 저장되어 있기 때문에 각 비트에 맞춰서 분류하는 작업이 필요합니다.
(1) 부동소수점 전용 공용체(union)선언
- 공용체의 메모리를 공유한다는 특성을 이용할 계획입니다.
( 공용체관련 포스트 🖝🖝 [C]공용체(Union) )
< t_fltp (floating point 공용체) >
typedef union u_fltp
{
double storage; // 직접 값을 받아오는 변수
struct
{
unsigned long long int mant :52 ;
unsigned short expt :11 ;
unsigned char sign :1 ;
} bit;
} t_fltp;
(2) t_fltp공용체 동작 확인 테스트
- 임시로 테스트 함수를 만들어서 부호비트, 지수부, 가수부로 잘 나누어져서 출력되는지 확인했습니다.
< t_fltp공용체 테스트 출력 ( -7.25 )>
void check_float(double n)
{
t_fltp of;
unsigned char result1;
unsigned short result2;
unsigned long long int result3;
of.storage = n; // (double)of.storage
result1 = of.bit.sign;
printf("Significant: %d\n", result1);
result2 = of.bit.expt;
printf("Exponent: %d\n", result2);
result3 = of.bit.mant;
printf("Mantissa: %lld\n", result3);
}
int main(void)
{
check_float(-7.25);
}
Significant: 1
Exponent: 1025
Mantissa: 3659174697238528
- -7.25을 테스트 값으로 넣었습니다. 7.25는 1.1101(2) x 2^2로 표현할 수 있습니다.
- 부호비트에 정상적으로 1이 들어가 있습니다.
- 64비트 기준 지수부는 1023( = 2^0)기준으로 음수지수 양수지수로 나눠집니다. 2^2이므로 1025( 1023 + 2)가 지수부에 정상적으로 들어있음을 확인했습니다.
- 가수부에도 2^51 + 2^50 + 2^48값인 3659174697238528이 정상적으로 들어있음을 확인했습니다.
3️⃣ 부동소수점(부호비트, 지수부, 가수부)출력
(1) 부동소수점의 정수부분까지 복사하는 함수 구현
< va_arg_f함수 >
void va_arg_f(va_list ap, t_flag *fg)
{
t_fltp of;
int cnt;
int move; // 움직일 비트칸 수
unsigned long long int man;
cnt = 0;
of.storage = va_arg(ap, double); // 매개변수포인터에서 double형으로 받아옴
move = of.bit.expt - 1023; // -1023하여 승수를 판단
if (of.bit.sign == 1) // 음수일 때
{
fg->fl_result[0] = '-';
of.bit.sign = 0; // 전체적으로 비트를 움직일때 영향력 없애기위해
cnt++;
}
of.bit.expt = 1; // 지수부분을 판별하고나면 1.xxx형태로 만듬
if (move < 0) // 지수가 마이너스일 때
{
of.bit_move = of.bit_move >> move; // 오른쪽으로 move만큼 비트이동
fg->fl_result[cnt++] = '0';
fg->fl_result[cnt++] = '.';
}
else // 지수가 음수가 아닐 때
{
of.bit_move = of.bit_move << move; // 왼쪽으로 move만큼 비트이동
fg->ulli = of.bit.expt;
ft_ullitoa_cpy(fg->ulli, DIGITS, &(fg->fl_result[cnt])); // 정수부분
cnt = ft_strlen(fg->fl_result);
fg->fl_result[cnt] = '.';
cnt++;
}
man = of.bit.mant; // 소수 부분 대입
ft_ftoa(man, &(fg->fl_result[cnt])); // 소수부분을 문자열로 복사하는 함수
}
- 문자열화된 부동소수점의 결과를 저장하기 위해
t_flag구조체에char fl_result[70];로 선언하였습니다. (부동소수점의 크기를 넉넉하게 70으로 잡았습니다. ) - 먼저
of.bit.sign으로 부호를 판별하여 문자열로'-'을 복사했습니다. move변수를 통해 지수를 판별하여of공용체의 전체 비트의 위치를 조절해 주었습니다.- 부동소수점의 정수부분은 기존에 구현한
ft_ullitoa_cpy함수를 이용하여 복사했습니다. - 소수점부분은 다소 복잡하기 때문에 새로운 함수인
ft_ftoa에서 처리하도록 구현했습니다.
(2) 부동소수점의 소수부분을 복사하는 함수
< ft_ftoa함수 + ft_set_float함수 >
static void ft_set_float(double fl, char *str)
{
int cnt;
cnt = 0;
while (cnt < 16) // 십진 소수점이 최대 소수점 자리수는 16
{
fl *= 10;
str[cnt] = (int)fl + '0'; // 일의자리수를 저장
fl = fl - (int)fl;
cnt++;
}
}
static void ft_ftoa(unsigned long long int fl, char *str)
{
double temp = 0;
unsigned long long int nb = 1;
int i;
i = 52;
while (i-- > 0) // 이진수 소수점의 일의자리는 1 / (2^52)를 뜻함
nb *= 2;
while (fl > 0)
{
if (fl % 2 == 1)
temp = temp + 1 / (double)nb;
fl /= 2;
nb /= 2;
}
ft_set_float(temp, str);
}
ft_ftoa함수에서 지수를 고려하여 비트이동된 가수부부분을 십진수 소수로 바꿔주는 함수입니다.ft_set_float함수를 통해서 십진수 소수를 문자로 바꿔서 최종적으로 복사해줍니다.
4️⃣ 실수형 출력 비교 테스트
- 아직 실수형서식지정자의 플래그, 각종 옵션의 적용한 코드를 구현하지 않았지만 기본적인
%f출력에 대해 테스트를 해보았습니다. - 임시로
test_print_f함수를 구현하였습니다. ( 추후에 e, g서식 지정자를 추가하여 제대로 구현할 예정입니다. )
< test함수 + main함수 >
void test_print_f(char *format, ...)
{
va_list ap;
t_flag fg = { 0, };
va_start(ap, format);
{
va_arg_f(ap, &fg);
}
va_end(ap);
printf("%s\n", fg.fl_result);
}
int main(void)
{
va_list ap;
test_print_f("test", -7.251131);
printf("%.16f\n",-7.251131);
}
-7.2511309999999999
-7.2511310000000000
- 구현한 f 서식지정자 출력함수와
printf함수와 비교했습니다. - 가수부가 52비트임을 고려하면 나올 수 있는 십진법 소수점자리수가 소수점 16번째자리 수 임을 고려하여
printf함수의 서식옵션에.16을 적용 하였습니다. - 부동소수점을 문자형으로 변환하는 과정에서 위의 테스트 결과와 같이 어쩔 수 없이 오차가 생겼습니다.
printf함수의 결과와는 다르게 나타났습니다. 그래서 다른조건을 적용하여 아래와 같은 결과를 얻었습니다.
int main(void)
{
printf("%.30f\n", -7.251131);
}
-7.251130999999999993121946317842
printf함수의 기존의 테스트 옵션을.16에서.30으로 변경하여 출력해 봤습니다.- 출력결과를 보면 알 수 있듯이 내장함수
printf함수 역시 오차가 생긴 것을 알 수 있습니다. 처음 테스트 케이스같은 경우 우연히.16옵션에서 반올림 처리가 된 것 이였습니다. - 하지만 기존에 생각했던 소수점 16자리보다 더 정밀하게 출력이 가능했습니다.
- 구현한 f서식지정자 함수의 소수점 자리수 출력을 다시 점검해야할 필요가 있을 것 같습니다.
